
Five-Block Theory
In every completed Riichi Mahjong hand (with the exception of Seven Pairs and Thirteen Orphans), every hand consists of 4 sets of three tiles and 1 pair of two tiles (therefore, 5 blocks).
Five-block theory is a method of maximizing tile efficiency – working backwards from hand shape to get rid of the most redundant tile in your hand.
Scenario 1
Imagine that it’s your turn and you have this hand. What would you discard?

Using five-block theory, let’s split this hand into five blocks:
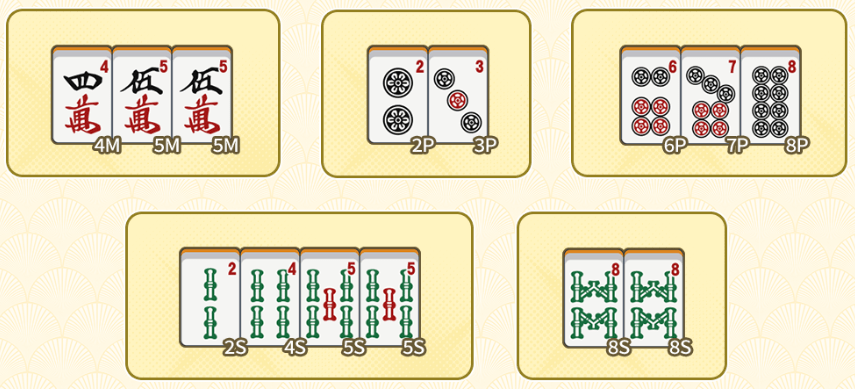
Now, let’s examine each of the 5 blocks we have:
- [4m 5m 5m] → This block has the possibility of accepting [36m] to form [345m] or [456m]. However, this block also has the possibility of drawing another [5m] to form a [555m] block. Therefore, we should keep this block intact for now.
- [2p 3p] → This block is waiting to accept [1p] or [4p] to form a completed block.
- [6p 7p 8p] → This block is already completed, so there’s no need to touch it.
- [8s 8s] → This looks like our potential pair, and there’s no need to touch it for now.
- [2s 4s 5s 5s] → Note that the [2s] is a redundant tile. Without the [2s], the [455s] block can still accept [3s], [6s], or [5s]. Even if you draw a second [2s] later, it does not help progress your hand.
Therefore, the correct discard is [2s].
Scenario 2
Imagine that it’s your turn and you have this hand. What would you discard?

Splitting this hand into blocks:
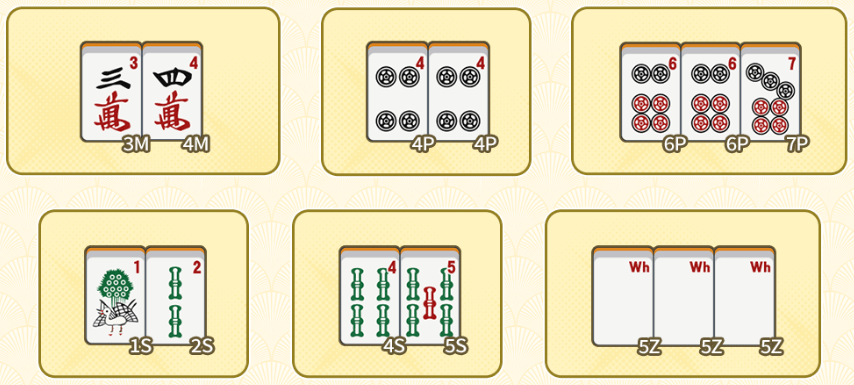
Notice that there are 6 blocks instead of 5, which means we have a block surplus!
Again, let’s examine each of the blocks we have:
- [3m 4m] → This block is waiting to accept [2m] or [5m] to form a completed block.
- [4p 4p] → This looks like our potential pair, and there’s no need to touch it for now.
- [6p 6p 7p] → For the same reasons mentioned above, we should keep this block intact for now, to maximize acceptance of [5p], [6p], and [8p].
- [4s 5s] → This block is waiting to accept [3s] or [6s] to form a completed block.
- [5z 5z 5z] → This block is already completed, so there’s no need to touch it.
- [1s 2s] → This block is waiting for [3s] to form a completed block. Note that this block has overlapping tile acceptance (ukeire) with the [45s] block mentioned above. Therefore, this block is redundant.
As a general rule of thumb, when your blocks are fixed, you should discard redundant tiles from the inside out. Therefore, you should discard [2s] first, before [1s]. This is because inside tiles tend to be more dangerous than outside tiles, so you want to get rid of them earlier to avoid future problems.
Wrapping up
In summary, here’s a step-by-step guide on how to apply five-block theory:
- Divide your hand into five blocks
- Compare each of the five blocks
- Find the most redundant tile, and discard it
Five-block theory may seem confusing at first, but the key is to practice enough such that it becomes second nature to you!
Six-Block Theory
The five-block theory we just covered maximizes tile efficiency. However, there are situations where we can split our hand into six blocks instead of five.
Although the six-block theory loses a bit of tile efficiency, it allows you to postpone your choice of which block to discard, and let you decide later once you have more information.
Both the five-block and six-block theory have benefits and drawbacks, and both can be used depending on what our hand needs.
Scenario 1
Imagine that it’s your turn and you have this hand. What would you discard?

Using five-block theory: discard [3m] or [3p]
[6m 7m 7m] → This block has the possibility of accepting [58m] to form [567m] or [678m]. However, this block also has the possibility of drawing another [7m] to form a [777m] block. Therefore, we should keep this block intact for now.
[9p 9p] → This looks like our potential pair, and there’s no need to touch it for now.
[2s 3s 4s 5s 6s] → This can be seen as 2 blocks, either:
- [2s 3s 4s] + [5s 6s] or [2s 3s] + [4s 5s 6s]
Either way, these 2 blocks form a strong shape that can accept [1s], [4s], and [7s] to form 2 completed shapes.
[2m 3m] and [2p 3p] → Using five-block theory, only one of these blocks can be the 5th block. Therefore, the other block will be redundant.
Get rid of one block by discarding either [3p] → [2p], or [3m] → [2m]. This decision would depend on certain other factors. For instance, if [1p] or [2p] was the dora, you might want to discard the [23m] block over the [23p] block, to increase the potential value of your hand. Alternatively, if many of the [1m] and [4m] tiles have been discarded, the chance of drawing [1m] or [4m] is lower, so you might want to discard the [23m] block over the [23p] block.
Using six-block theory: discard [7m]
[9p 9p] → This looks like our potential pair, and there’s no need to touch it for now.
[2s 3s 4s 5s 6s] → This can be seen as 2 blocks, either:
- [2s 3s 4s] + [5s 6s] or [2s 3s] + [4s 5s 6s]
Either way, these 2 blocks form a strong shape that can accept [1s], [4s], and [7s] to form 2 completed shapes.
- [2m 3m] → Keep this block to potentially accept [1m] or [4m]
- [2p 3p] → Keep this block to potentially accept [1p] or [4p]
[6m 7m 7m] → Discarding the [7m] here only loses 2 tiles of acceptance (the last 2 [7m] tiles, to form a [777m] shape). Depending on what you draw afterwards, and with more information as the match progresses, you can then postpone your choice of which of the following blocks to discard: [23m], [23p], or [67m].
Personally, I would choose the six-block method over the five-block method in this case, and discard [7m]. This guarantees a pinfu hand and also keeps the possibility of [123] or [234] sanshoku alive. This also lets me postpone my choice of which ryanmen wait to discard, depending on the board state.
Scenario 2
Imagine that it’s your turn and you have this hand. What would you discard?

Using five-block theory: discard [1m] or [8m]
[3p 4p 0p 6p 7p] → This can be seen as 2 blocks, either:
- [3p 4p 0p] + [6p 7p] or [3p 4p] + [0p 6p 7p]
Either way, these 2 blocks form a strong shape that can accept [2p], [5p], and [8p] to form 2 completed shapes.
[4s 0s 5s] This block has the possibility of accepting [3s] to form [345s] or [456s]. However, this block also has the possibility of drawing in another [5s] to form a [555s] block. Therefore, we should keep this block intact for now.
[9s 9s] → This looks like our potential pair, and there’s no need to touch it for now.
[1m 3m] and [6m 8m] → Using five-block theory, only one of these blocks can be the 5th block. Therefore, the other block will be redundant.
Get rid of one block by discarding either [1m] → [3m], or [8m] → [6m]. This decision would depend on certain other factors. For instance, if [1m] or [3m] was the dora, you might want to discard the [68m] block over the [13m] block, to increase the potential value of your hand. Alternatively, if many of the [7m] tiles have been discarded, the chance of drawing [7m] is lower, so you might want to discard the [68m] block over the [13m] block.
Note that since both of these shapes have a chance to improve further into a ryanmen wait, you should discard tiles from the outside in, thus the [3m] and [6m] should not be discarded first! For example, if you discard 8m and you draw [5m] in the next turn, your [56m] shape now becomes stronger than your [13m] shape, and you can then discard [3m] followed by [1m].
Using six-block theory: discard [5s] to postpone your choice of which of the two bad-wait blocks to discard.
[9s 9s] → This looks like our potential pair, and there’s no need to touch it for now.
[3p 4p 0p 6p 7p] → This can be seen as 2 blocks, either:
- [3p 4p 0p] + [6p 7p] or [3p 4p] + [0p 6p 7p]
Either way, these 2 blocks form a strong shape that can accept [2p], [5p] and [8p] to form 2 completed shapes.
- [1m 3m] → Keep this block to potentially accept [2m]
- [6m 8m] → Keep this block to potentially accept [7m]
[4s 0s 5s] → Discarding the 5s here only loses 2 tiles of acceptance (the last 2 [5s] tiles, to form a [555s] shape). Depending on what you draw afterwards, and with more information as the match progresses, you can then postpone your choice of which of the following weaker blocks to discard: [13m] or [68m].
Here, the decision on whether to use the five-block method or six-block method is not so clear-cut. Discarding [1m] or [8m] accepts more types of tiles than discarding [5s], and there is an argument for using both the five-block or six-block methods here.
Personally, I would still choose the six-block method over the five-block method in this case, and discard [5s]. This allows me to try and aim for a pinfu hand, and wait for more information before deciding which shape to discard later.
I sincerely hope this was helpful. Good luck to you!





Be the first to comment