I had assumed that a 10×10 grid was best, but it turns out it’s not.
Contents
Guide to The Optimal Square Grid
All credit goes to me22ca!
Introduction
I always figured that if I was going to build a nice, regular, square grid that of course it should be 10×10: That way each of the blocks is fully zonable and the road length highlight and road guideline circles make it easy to draw.
But it turns out we can do better.
Time for Mathematics
For the 10×10 grid, the calculation is simple: we get 8² zonable tiles in a 10² tile area, for a density of exactly 64%. (Here, and in the rest of the section, we assume a small—2u—road).
For the general case of a square of side ?, the zoneable area is (?-2)²-max(0, ?-10)² — the area inside the road minus the area in the middle where the zoning doesn’t reach — and the total area is ?².
It’s hard for me to grok that quotient in my head, so let’s just graph it and see what happens:
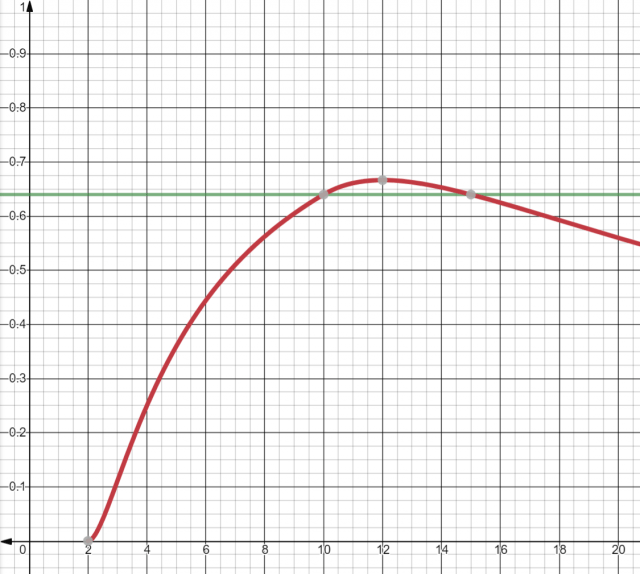
That shows that the “obvious” 10×10 grid is actually only as good as a 15×15 grid:
It also looks like 12u is the best. Can we prove it? Sure, let’s go back to Calculus I:
- 0 = d/d? (?-2)²-(?-10)² / ?²
- 0 = d/d? ( (?-2)+(?-10) )*( (?-2)-(?-10) ) / ?²
- 0 = d/d? (2?-12)*8 / ?²
- 0 = d/d? (16?-96) / ?²
- 0 = ( (16)*?² – (16?-96)*2? ) / ?⁴
- 0 = (16? – 32? + 192) / ?³
- 0 = -16? + 192
- ? = 192/16
- ? = 12
So yes, it’s a block length of exactly 12 that gives the best density.
Note: Coincidentally, that’s also the maximum segment length for an axis-aligned road in CSL.
How much better? ⅔ of the area (66.66…%) instead of just 64%.
Now, I admit that only about 4% more zoning doesn’t sound that exciting. But not only is it more dense, but it’s also cheaper.
How’s that? Well, you need to pay for the roads. And for the 10×10 blocks, those 64 tiles of zoning need 40u of roads (1.6tiles/u), but with a 12×12 block you get 96 tiles of zoning out of only 48u of roads (2tiles/u). So you’re also paying 16% less on the roads to grid the same area with more stuff.
For some concrete numbers, let’s compare a 60×60 area (as it divides evenly in a bunch of ways) using a variety of block sizes and the basic small two-lane road:
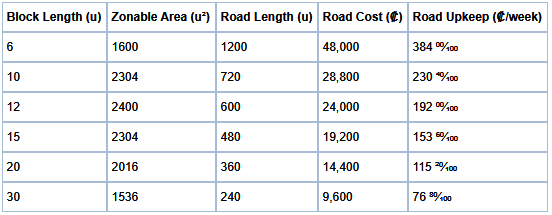
So if you make a 10×10 grid, you’ll spend 50% more than you need to for the area you’ll get.
Note: That table also shows that zonable area drops slower than road cost, but don’t forget that lower density is also increased cost for any service with a radius of effect.
Conclusion
If you want the densest square grid, make it 12×12 (using small roads).
You’ll fit 1⁄24 more RICO in the same space but spend 1⁄6 less on the roads, compared to a 10×10 grid.
Appendix A: Medium or Large Roads
What if you’re using a 4u-wide road, like the Medium and Large Roads?
Then the optimal-density square grid is 16×16.
But you pay a heavy density price for the larger roads: only 50% of the area is usable for zoning.
Appendix B: Rectangles
Rectangles, as they get longer and longer, can arbitrarily approach the limit† of 80% density.
The density formula for an α×β block is ((α-2)(β-2) – (α-10)(β-10))/(αβ), assuming both sides are 10-or-longer for simplicity (it’s clear that if both are smaller than 10 it’s worse than the square, and I don’t care what happens for silly things like a 5×50 block).
So there’s a surprising amount of choice if you just want to do better than the 10×10 block:
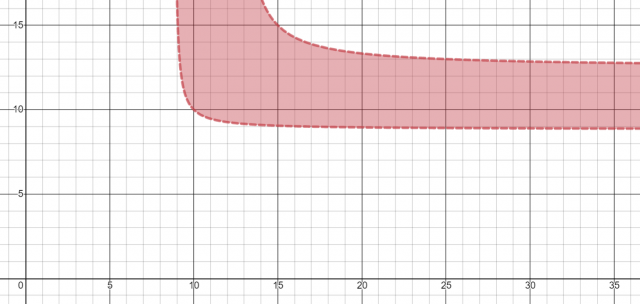
But your choices are far more limited if you want to beat a 12×12 block:
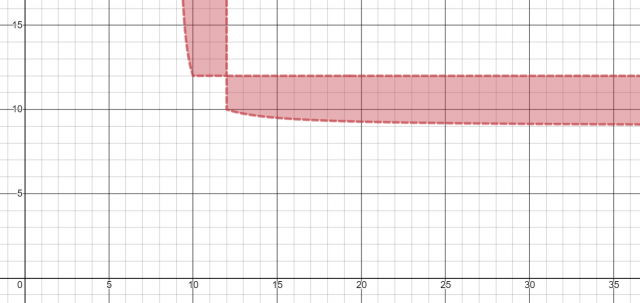
Indeed, if you restrict yourself to integers (so you can draw it with Snap to Road Length), then the only things that beat the best square block are α ∋ {10, 11}, β ∋ {13, 14, 15, …}.
How much better? Well, 10×16 has a density of 70%, an extra 5% more than the 12-square. Getting up to 75% density takes 10×32, which is more oblong than I personally like for a grid.
Is the extra density worth being less regular? I’ll leave that up to you.
The limit is parallel lines that are infinitely long and never connected, as that way there’s never any potentially-zonable area taken up by a cross street. A quick look at the cross-section of such a road shows 4u zoneable on each side and a 2u road, for (4+4)/(4+2+4)=0.8 density.
Appendix C: Real Cities
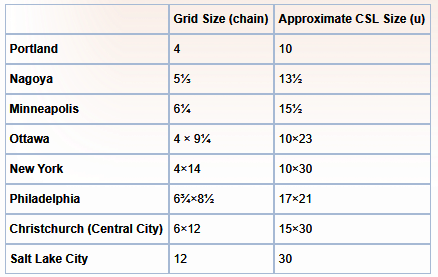
These are measured from satellite maps, so don’t always match the “canonical” answers. For example, the Portland Bureau of Transportation says its blocks are 200ft (≈7.6u).
Your mathematics about the city blocks/grids are sincerely insightful and helpful! I will definitely apply them into my city builds.
I have also personally done some comparative searches about city grids and city size before;
Brilliant guide, thanks for sharing it!
I get a little bored of loads of squares and like to mix up the roads and looking at the heterogeneous roads gave me and idea on hereogenuous rectangles. I’m mot sure on the maths (and clearly you are!) but would a 11×26 (therefore 8×23 zoneable) give an almost 64% density? I know it’s still not as efficient normal rectangles, but better than the square and deals with my aesthetic ‘itch’ to avoid squares?
Now that’s got me thinking… what about squares with chamfered edges, like Barcelona? Or hexagons which would leave squares in between them!? God knows what the calculations would be to figure that out
Thanks! I actually started doing this same grid size some time ago, exactly minding the buidable area after a possible road upgrade.
Personally, I’d consider a developing a calculator that has the maths here built in, though I’m not sure of the interest to design, mix-and-match, plan, and verify your grid setup before placing it. It’d probably be a client-side JS webpage you can run on the web or download locally (as html).
Further, terrain limitations and re-aligning to grid when there’s a gap in your city (e.g., an industry area in a separate, directly-connected area, harbor, airport, etc) can make a always ensuring you don’t box-out your zoning spaces with dead tiles can be difficult and even with this solution there isn’t always a direct solution with a ploppable or zoneable object, or changes to the networks.
I’ve always done 8×8 square blocks but I do like the 16×16 method, having the 4×4 open in the center I could fill with Trees to help with noise polution, I’m gonna try it on my next city
Road grids have their place and SoCal is a classic example of this where I could drive from Tustin to Anaheim or points north, without having to get on the interstate.
In Appendix B, each axis is one side of the rectangle, and the colored area is more efficient than a 10×10 and 12×12 respectively. The very first graph you see (in the section labeled “time for mathematics”) is for squares, where the Y axis is density, and the X axis is square side length.
I had nothing to do with the creation of this guide, but I hope that helps.
There is another useful consideration: Having the lengths be Pythagorean triples (or almost triples, the game gives a tiny bit of leeway) allows you to join non-perpendicular grids together without having odd half-squares and gaps at each road.
The most useful ones are probably 12:16:20, 9:12:15, 8:15:17 and 5:12:13 (possibly skipping every other road in the latter ones, for 18×12, 16×15 and 10×12).
Note that these distances are between the centers of intersections.
In my actual city I tried 10×40 with small roads in most blocks, and only in commercial/industrial blocks which need also truck traffic, I add an additional 6laneroad which splits the 10×40 into 2 10×20 blocks. The only road which is having traffic jams, is the 6lane road, which I think is because it is “sucking” traffic from the small roads because it is theoretically faster, and it has crossing every 10 units, which reduces the real speed. Therefore I am thinking about removing every second crossing by cutting the small roads by 3, or perhaps building an underground highway underneth it.
For rectangular blocks, 8*infinity is obviously the best.
By the way, re-reading this thread (I totally forgot what it was about) I just realized both are correct:
>8*x